Аннотация: В данной статье рассматривается возможность сжатия данных при использовании скелетной анимации. При этом используется квантование данных анимации во времени — положение, угол поворота и размер. Рассмотрено использование различных кривых и сделан вывод о результатах полученной оптимизации.
Научный руководитель: Харламенков А. Е.

Проблема

Во время работы над магистерским проектом по созданию «Системы визуализации русско-жестового перевода» [8-21] была выявлена проблема ограниченности ресурсов при запуске программы на мобильной платформе. После определения того, сколько ресурсов потребляет программа, был сделан вывод, что наиболее ресурсоёмкий процесс — работа с анимацией. Далее для решения проблемы с производительностью и памятью было проведено исследование по сжатию анимационных данных.

Жестовый язык насчитывает более 70 базовых конфигураций кистей рук и более 300 анимаций движений рук и всего остального тела (включая мимику и неявные микродвижения). Со временем база жестов пополняется, продолжается внедрение и редактирование базы данных жестов. [17]

Способы решения

Есть два способа решения проблемы с памятью при разработке приложения: сделать динамическую подгрузку анимации; оптимизировать данные анимации. В итоге был выбран второй пункт, потому что анимация в нашем случае комплексная, и динамическая подгрузка будет выполняться достаточно долго (с учётом использования мобильного устройства, и того, что многие жесты состоят из множества различных анимаций). Кроме того, оптимизация анимационных данных уменьшить размер базы данных и приложения. Это позволит сэкономить на мощности сервера (при загрузке базы данных жестов), и приложение будет занимать меньше места на устройстве пользователя.

К оптимизации и сжатию анимационных данных можно подойти разными способами. В этой статье будет рассказано о двух основных методах: квантовании и подгонке кривой. Сжатие всегда приводит к компромиссу между уменьшением качества и оптимизацией памяти, поэтому далее в исследовании учитывается то, что в итоге после сжатия анимация должна быть приемлемой и понятной при просмотре. Также был рассмотрен вопрос организации данных для максимального увеличения производительности.

Введём несколько определений, знаний которых необходимо при рассмотрении вопросов оптимизации анимаций. Кватернионы предоставляют удобное математическое обозначение положения и вращения объектов в пространстве. В сравнении с углами Эйлера, кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси, независимо от совершенного вращения по другим осям. В сравнении с матрицами они обладают большей вычислительной устойчивостью и могут быть более эффективными благодаря чему и нашли своё применение в компьютерной графике. [1]

Сплайн — это функция, область определения которой разбита на конечное число отрезков, на каждом из которых она совпадает с некоторым алгебраическим многочленом (полиномом). Максимальная из степеней использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. [2]

Квантование

Квантование — разбиение диапазона значений временных отсчётов сигнала на конечное число уровней и округление каждого отсчёта до одного из двух ближайших к нему уровней.

Квантование — это процесс процесс приведения значений из непрерывного набора возможностей к относительно небольшому дискретному множеству. Скелетная анимация хранит в себе данные о положении, углах поворота и размерах. Процесс квантования трёхмерных векторов, которые используются для представления положения и размеров, не является сложным. Он осуществляется путём получения их максимальных и минимальных значений и равномерного разбиения значений в данном диапазоне. Однако большая часть качественных анимационных клипов задействует поворотный механизм.

Мы используем кватернионы для представления поворотов в трёхмерном пространстве. Наш подход к квантованию данных вращения использует определённые математические свойства кватернионов. Пусть единичные кватернионы, где все компоненты находятся в диапазоне [-1,1], тогда необходимо найти составляющую x, y, z или w, имеющую наибольшую абсолютную величину. Затем отбрасывается этот компонент и сохраняются остальные три, поскольку это позволит легко вычислить пропущенную компоненту, используя тот факт, что единичные кватернионы удовлетворяют равенству (1).

Опуская самую большую компоненту, можно ограничить диапазон оставшихся трёх до (2),

так как в единичном кватернионе компонент вне этого диапазона должен иметь наибольшее абсолютное значение и, следовательно, быть компонентом, который можно было опустить. Далее максимизируется точность путём квантования в меньший диапазон, чем [-1, 1], который является диапазоном, который можно было бы использовать, если бы не был исключён самый большой компонент. Это также позволяет избежать восстановления компонента с небольшим значением, которое подвержено повышенной ошибке. [3]

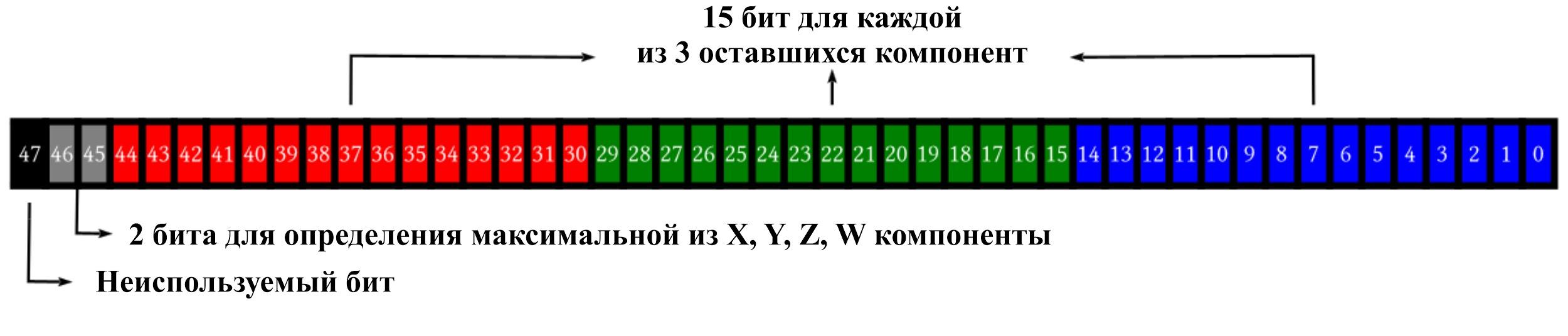
Рис. 1. Кватернион в памяти

Благодаря данному подходу, выделяются по 15 бит для каждого из трёх сохранённых компонентов и 2 бита для указания пропущенного компонента. Поэтому каждый кватернион занимает в общей сложности 48 бит (1 бит остаётся неиспользованным), как показано на рисунке 1. Для сравнения, необработанный кватернион использует 32-разрядное число с плавающей запятой для каждого из компонентов, что приводит к общему использованию 128 бит. При уменьшении от 128 бит до 48 бит достигается коэффициент сжатия 0,375.

Это 48-битное квантование кватернионов гарантирует точность в 0,000043. Такого результата достаточно для большинства случаев. Более того, когда был применён вышеописанный метод, не было замечено видимых потерь качества среди уже готовых анимаций. Также хотелось бы отметить низкую вычислительную сложность данного алгоритма, что несомненно является большим плюсом.

Настройка кривых

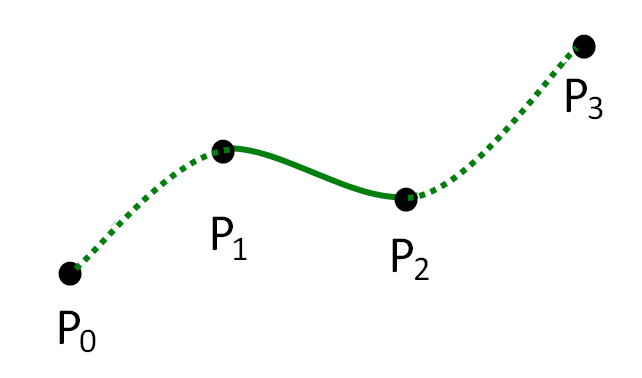
Рис. 2. Сплайн Catmull-Rom

Несмотря на отличные результаты предыдущего метода, результат нельзя считать до конца удовлетворительным. Поэтому рассмотрим ещё один метод дальнейшего сжатия с подгонкой кривой к изменяющимся значениям кватернионов. Это процесс построения кривой или математической функции, наиболее приближенной к ряду точек. В данном случае специально используются сплайны Catmull-Rom, которые можно представить как многочлен 3 го порядка. [4] Для определения отрезка сплайна Catmull-Rom необходимо четыре контрольных точки (см. Рис. 1).

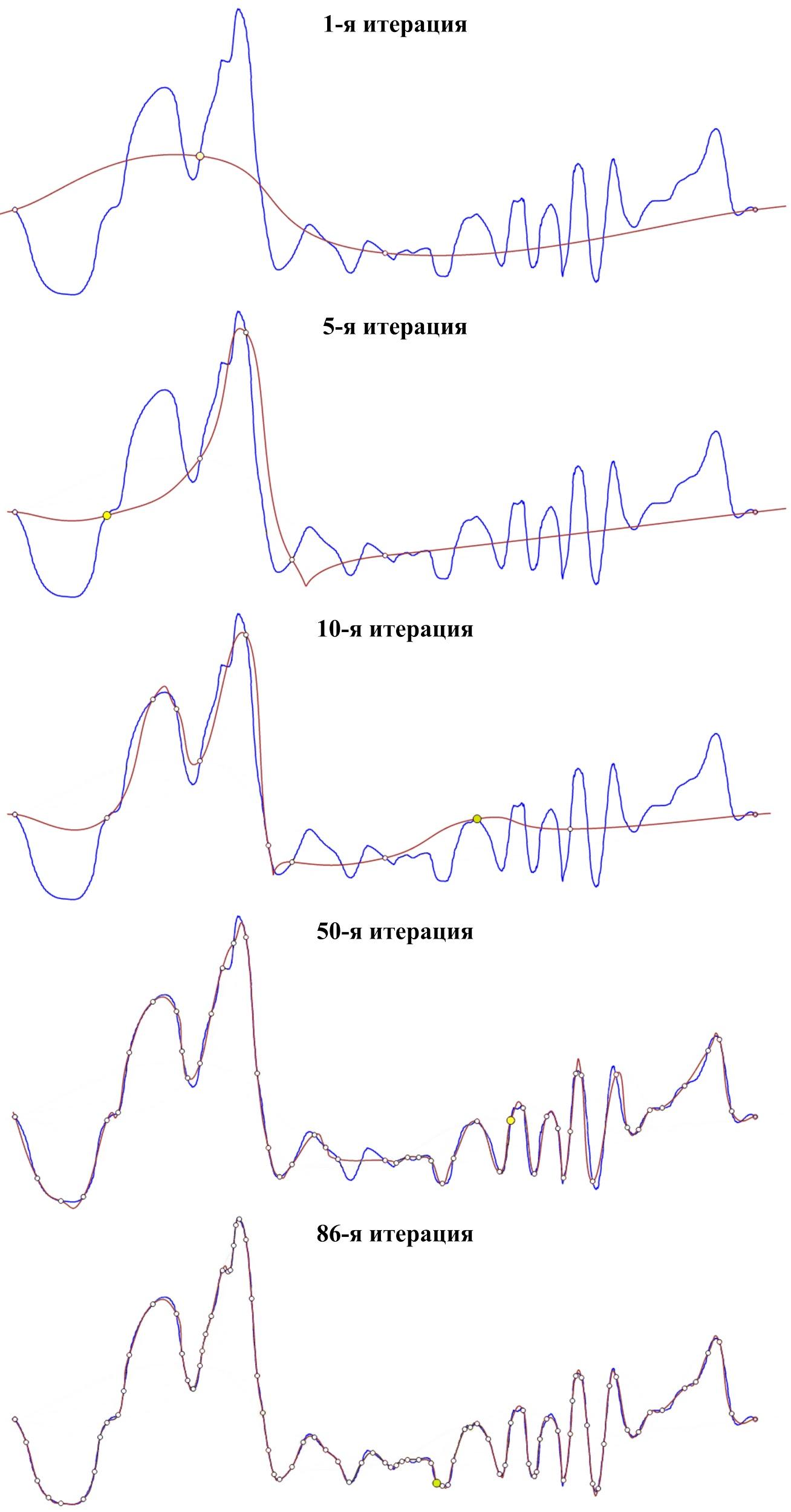
Рис. 3. 1-я, 5-я, 10-я, 50-я и последняя итерации

Подгонка сплайнов производится итеративно. Процесс начинается только с двух ключевых кадров, которые включают начало и конец рассматриваемой анимации. Далее необходимо с каждой итерацией добавлять больше ключевых кадров, чтобы снизить погрешности до максимально допустимого уровня. В ходе каждой итерации определяется отрезок между ключевыми кадрами с наибольшей погрешностью, а затем в середину данного отрезка выставляется новый ключевой кадр. Этот процесс вставки ключевого кадра в отрезок с наибольшей ошибкой повторяется до тех пор, пока ошибка для каждого отрезка не станет ниже заданного порога. [5] Часть итераций изображена на Рис. 3.

На рисунке выше можно увидеть, как кривая красного цвете постепенно приближается к исходной синей кривой. Жёлтые точки представляют собой дополнительные кадры на каждой итерации. В результате после 86 итераций из исходных 654 кадров было получено 90 кадров.

В результате настройки кривых квантованные результаты удалось сжать в разных случаях до 25%-75% от изначальных. Решающее значение в вопросе максимального сохранения исходного качества при значительной степени сжатия играет роль правильный выбор пороговых значений ошибок для данных о положении, вращениях и размерах.

Снижение потерь

Наиболее заметным артефактом, который возник из-за сжатия, было смещение положения конечностей в тех анимационных клипах, где они должны быть неподвижными. Эта ситуация возникает ввиду того, что происходит накопление ошибки, поскольку анимация родительских элементов влияет на анимацию дочерних узлов.

Одним из способов избавиться от подобной ошибки является использование адаптивных уровней ошибки. Суть их заключается в том, что допустимое значение ошибок зависит от количества дочерних элементов у объекта. Таким образом, чем больше дочерних элементов, тем ниже будет уровень допустимой для данного узла ошибки. Допустим, что для конечного элемента цепи устанавливается определённый порог. Для его родительского элемента порог уменьшается в 3 раза и так далее вверх по цепочке до корневого элемента. Данный подход позволяет снизить эффект накопления, хотя и частично снижает эффективность применяемого сжатия.

Есть также и другой, достаточно простой и эффективный подход, называемый пиннингом. Данное понятие происходит от английского “pin” — приколоть. Он заключается в том, что при сжатии данных конечность как бы прикалывается к изначальной позиции и не зависит от изменений в родительских элементах. [6]

Эффективная организация данных

Наконец, рассмотрим способы эффективного использования методов, описанных ранее в данной статье. В процессе работы над ними было важно помнить о возможных утечках памяти, которые могли бы крайне неприятно сказаться на производительности после определённого времени использования. Поэтому было принято решение организовать данные таким образом, чтобы оптимизировать работу с кэшем.

Для начала, было принято решение о том, что все ключевые кадры, то есть кадры хранящие информацию о положении, вращениях и размерах каждого сустава, были объединены в единый непрерывный блок памяти. Одной из распространённых практик является создание отдельного блока памяти для каждого канала в суставе, но такая, казалось бы, естественная организация может стать причиной ошибок в кеше при расчёте полной позы скелета в определённый момент времени. Можно было бы поместить данные в один блок, потому что полезная нагрузка составляет 48 бит для всех типов каналов. Как уже было упомянуто ранее, в процессе сжатия было произведено квантование кватернионионов до 48 бит, а также квантование 3D-векторов позиции и размеров на одинаковое количество бит, назначая 16 бит каждому из компонентов x, y и z. Листинг 1 представляет код полученной структуры.

Листинг 1. Код структуры CompressedFrame

В вышеуказанном листинге (Листинг 1) производится квантование ключевое время до 16 бит. Переменная jointIndex указывает, к какому соединению относятся данные этого кадра. Массив v содержит квантованную полезную нагрузку. Важное значение имеет различие в отношении полезной нагрузки для позиции, вращения или масштабирования. Для этого используются два наиболее важных бита jointIndex для этого. Использование этих битов таким образом ограничивает jointIndex до 14 бит, или 16384 общих суставов, что, безусловно, достаточно для анимирования человека и в частности его кистей, которые обычно требуют менее 250 суставов (для 210 костей).

Правильный порядок ключевых кадров становится критическим, независимо от типа соединения или канала, в одном отделении. Их можно просто упорядочить по ключевому времени (keyTime), но при этом возникают проблемы. Можно представить то, что происходит во время выполнения анимации (Рис. 2).

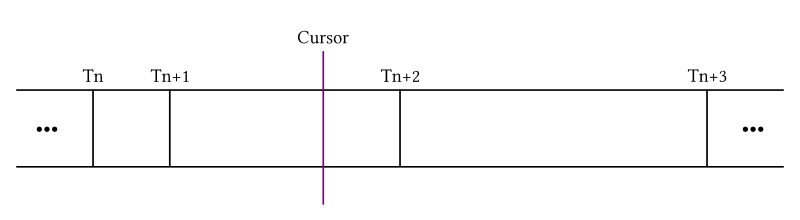
Рис. 4. Пример отделения с ключевыми кадрами и курсором, который указывает на позицию между Tn+1 и Tn+2

Предположим есть четыре ключевых кадра (отсортированные по времени ключа keyTime) и курсор (Cursor) времени, который обозначает текущее время воспроизведения. Необходимо получить информацию о Tn, Tn + 1, Tn + 2 и Tn + 3, потому что для оценки сплайна требуется четыре контрольных точки. Учитывая, что текущая позиция курсора прошла мимо Tn и Tn + 1, курсор должен уже знать о них. Что относительно Tn + 2 и Tn + 3, которые лежат в будущем с точки зрения курсора? Можно предположить, что их можно быстро просканировать линейно, так как это следующие два кадра которые расположены друг за другом. [7]

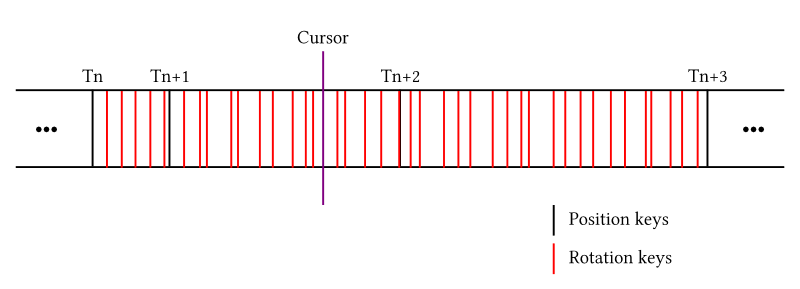
Рис. 5. Пример отделения с ключевыми кадрами и курсором, который указывает на позицию между Tn+1 и Tn+2 с обозначением ключей вращения

Однако этот подход не является оптимальным. Скажем, эти Ts являются позиционными кадрами. Может существовать какое то количество кадров вращения между двумя соседними кадрами позициями (как вы можете видеть на рисунке 5), если анимация происходит в основном из вращательных движений. Это связано с тем, что все кадры размещаются в одном отделе, поэтому линейное сканирование для поиска Tn + 2 и Tn + 3, вероятно, будет неэффективным.

В итоге одно из решений, чтобы воспроизвести анимацию за один проход (при этом возможно кеширование, что сильно повышает производительность) — расположить кадры по тому, когда они нужны, а не по времени кадра. Для этого нужно получить информацию Tn + 2, как только курсор проходит ключевое время Tn; поэтому нужно расположить Tn + 2 на основе времени ключевого времени Tn. Размещённый таким образом, в любой момент курсор обеспечивает всю информацию, необходимую для текущей оценки, поэтому кэш-пропуски могут быть сведены к минимуму. Диаграмма на рисунке 6 показывает, как это упорядочение работает в случае анимации, состоящей из четырёх клавиш положения и девяти поворотных ключей.

Рис. 6. Расположение кадров по времени и расположение кадров по релевантности, по тому, в какой момент они нужны

Вывод

В среднем, метод квантования, который обсуждался в этой статье, уменьшил вдвое потребности в памяти. Можно сделать оптимизацию ещё сильнее, подобрав лучшую кривую, так как она требует предварительной обработки всех данных, но ранние результаты показывают, что она достигнет ещё 50% сжатия, а это значит, что оригинальные показатели использования памяти и производительности сокращаются до 25%.

Дополнительно можно исследовать многие направления, например, 32-битное (вместо 48-битного) квантование кватернионов, различные параметризации узлов для подгонки кривой, использовать метод наименьших квадратов вместо итеративного подхода, использовать усложнённую настройку того, как итеративный подход выбирает следующий ключ для добавления, и т. д.

Литература

1. КВАТЕРНИОНЫ [Электронный ресурс]: Большая российская энциклопедия — электронная версия. – Режим доступа: https://bigenc.ru/mathematics/text/2057671.

2. СПЛАЙН [Электронный ресурс]: Большая российская энциклопедия — электронная версия. – Режим доступа: https://bigenc.ru/mathematics/text/4247938.

3. Дискретизации и квантование цифрового сигнала. [Электронный ресурс]. – Режим доступа: http://lib.ru/TEXTBOOKS/TEACH/Physics/node25.html.

4. Introduction to Catmull-Rom Splines [Электронный ресурс]. – Режим доступа: https://www.mvps.org/directx/articles/catmull/.

5. Armstrong J. Catmull Rom Spline: TechNote / J. Armstrong. – № TN-06–001. – P. 10.

6. Autodesk Maya Online Help: Pin and unpin your character’s effectors [Электронный ресурс]. – Режим доступа: https://download.autodesk.com/us/maya/2009help/index.html? url=CSS_Pin_and_unpin_your_characters_effectors.htm, topicNumber=d0e319321.

7. Basics Of Maya Key Frame Animation — 3dtutorialzone.com [Электронный ресурс]. – Режим доступа: http://www.3dtutorialzone.com/tutorial? id=96.

8. Харламенков А. Е. Адаптация глухих и реакция социума / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2014. – Вып. № 2. – С. 269–273.

9. Харламенков А. Е. Аналитический обзор электронных on-line словарей жестовых языков: монография / А. Е. Харламенков. – Москва: РУСАЙНС, 2017. – 218 с.

10. Харламенков А. Е. Итоги издательской деятельности Института Непрерывного Профессионального Образования за 2010 — 2015 годы / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2015. – Вып. № 6 (6). – С. 423–439.

11. Харламенков А. Е. Итоги научной работы Института Непрерывного Профессионального Образования за 2010 — 2015 годы / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2015. – Вып. № 6 (6). – С. 413–422.

12. Харламенков А. Е. Короткие слова: предлоги, частицы, союзы. Справочник переводчика русского жестового языка: [Справочное издание]: Русский жестовый язык. Начала / А. Е. Харламенков. – Москва: Издательство «ОнтоПринт»,. – 154 с.

13. Харламенков А. Е. Методика преодоления безусловного рефлекса при постановке рук в процессе освоения дактильной и жестовой речи / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2014. – Вып. № 3. – С. 44–49.

14. Харламенков А. Е. Русский жестовый язык. Начала. Жестово-русский словарь: [Учебное пособие]: Русский жестовый язык. Начала / А. Е. Харламенков. – Москва: Издательство «ОнтоПринт»,. – 556 с.

15. Харламенков А. Е. Русский жестовый язык. Начала. Рабочая тетрадь: [Учебное пособие]: Русский жестовый язык. Начала / А. Е. Харламенков. – Москва: Издательство «ОнтоПринт»,. – 56 с.

16. Харламенков А. Е. Русский жестовый язык. Начала: [Учебное пособие]: Русский жестовый язык. Начала / А. Е. Харламенков. – Москва: Издательство «ОнтоПринт»,. – 164 с.

17. Харламенков А. Е. Создание «Электронной справочно-аналитической системы “Русско-жестовый толковый словарь”» Монография / А. Е. Харламенков // Научные труды Института Непрерывного Профессионального Образования. No 7. Монографические исследования / ред. Под научн. редакцией проф. П. С. Гуревича и проф. С. В. Чернова. С. 97–186. – Москва: Издательство Института Непрерывного Профессионального Образования, 2016. – С. 89.

18. Харламенков А. Е. Учебно-методическая разработка по курсу: «Основы русского жестового языка для разработчиков Жесто-мимического интерфейса “SurdoJet”» / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2015. – Вып. № 6 (6). – С. 337–366.

19. Харламенков А. Е. Формирование коммуникативной компетентности у людей с нарушением слуха / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2014. – Вып. № 4. – С. 234–241.

20. Харламенков А. Е. Электронная справочно-аналитическая система «Русско-жестовый толковый словарь» / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2014. – Вып. № 3. – С. 24–43.

21. Харламенков А. Е. Язык и менталитет: влияние жестового языка на менталитет глухих / А. Е. Харламенков // Научные труды Института непрерывного профессионального образования. – 2014. – Вып. № 5. – С. 191–218.

Корниенков Андрей Александрович
Магистрант Московского политехнического университета, г. Москва.
Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.

Рычков Вадим Александрович
Магистрант Московского политехнического университета, г. Москва.
Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.